TOPICS: Solutions Pythagoras Problems Solved Exercises Pythagorean Theorem
Problems
In the previous post we gave you various worked examples about the Pythagorean Theorem
where our goal was to calculate one of the sides of a right triangle (hypotenuse or leg) knowing
the measurements of the other two sides.

Now we’re going to look at some application problems for the Pythagorean Theorem in which
we must make use of our knowledge of this theorem to solve every day problems. We’ll see
that this theorem can be very useful for different problems that can come up in real life, like
calculating height or length with just a little information.
In the problems we have for you today, we’ll show you how, using the Pythagorean Theorem,
we can calculate the height of a triangle, the distance from the ground to the point where on
the wall where a ladder is leaning, the distance from the wall to the point on the ground where
the same ladder is standing or the length of a string.
As you can see, the Pythagorean Theorem helps us calculate distances and measurements in
real life, making it a mathematical theorem with a ton of interesting applications. Let’s see
some application problems and exercises for the Pythagorean Theorem that, aside from
being useful in daily life can also show up on a test, which is why it’s a good idea to master
these types of problems and exercises since they are common on many high school tests.
Below you can view the problems, 6 in total. First we have the solved exercises and then the
original problems (unsolved) in case you want to print them and practice these exercises and
problems on the Pythagorean Theorem yourself.
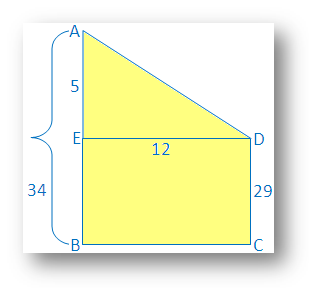
Solved exercises:
Pythagorean Theorem Application Problems Solutions
Unsolved exercises (to print and practice):
Pythagorean Theorem Application Problems
If you don’t know what homophone words are, the following link will help answer your
questions about homophone words.

Be the first to comment on "Pythagorean Theorem Application Problems"