Demostrar la veracidad de la expresión característica del teorema de Pitágoras es una tarea tan antigua como el descubrimiento del mismo teorema. Actualmente existen una gran cantidad de formas de demostrar que el teorema de Pitágoras es totalmente válido, algunas más famosas que otras.
En las siguientes líneas analizaremos las formas más relevantes que tienen por objetivo el demostrar que el teorema de Pitágoras es correcto.
Demostración del teorema de Pitágoras por Pitágoras
El propio Pitágoras presenta la demostración más famosa de este teorema en el que demuestra la igualdad utilizando la igualdad de las áreas generadas con las longitudes de los lados del triángulo rectángulo.
Demostración del teorema de Pitágoras por Euclides
La proposición I.47 de los elementos de Euclides hacen mención al teorema de Pitágoras y lo demuestra haciendo uso de áreas correspondientes a los lados del triángulo. Así, si trazamos una recta perpendicular a la hipotenusa y que pase por el ángulo recto además de tener 3 cuadrados con lados del mismo tamaó de cada lado del triángulo y que sean adyacentes a estos, tendremos que el área de cada cuadrado correspondiente a cada cateto es igual a la división correspondiente por la línea previamente trazada en el cuadrado de la hipotenusa.
Demostración del teorema de Pitágoras por Platón
Los ‘diálogos de Platón’ es un famoso compendio en el que también figura una demostración del teorema de Pitágoras basado en un triángulo rectángulo de 45° en los ángulos internos distintos al ángulo recto, es decir, en el uso de un triángulo rectángulo que además es isósceles.
Así también, existen demostraciones empíricas que basan sus cálculos en distintas situaciones cotidianas como el uso del agua para comprobar la veracidad de la demostración del teorema de Pitágoras propuesta por Euclides o el recorte de figuras geométricas que sean usadas como puzzles y gracias a las cuales se pueda demostrar el teorema de Pitágoras.
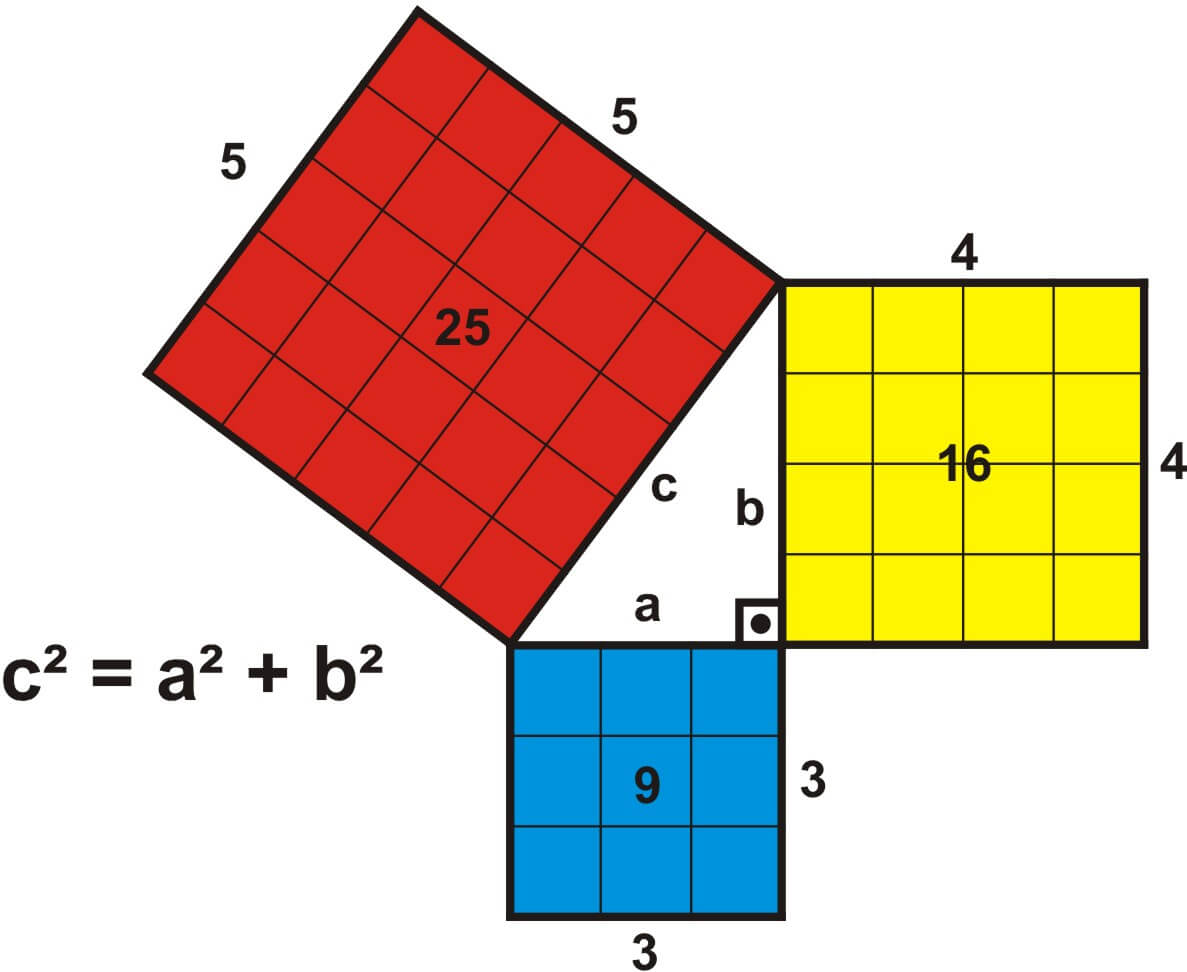
Esta me parece ser la mejor explicación que hay.